"PARES DE ÁNGULOS"
ÁNGULOS ADYACENTES
Son los que estan formados de manera que un lado es común y los otros dos lados pertenecen a la misma recta.
Son los que estan formados de manera que un lado es común y los otros dos lados pertenecen a la misma recta.

ÁNGULOS COMPLEMENTARIOS
Son dos ángulos que sumados valen un ángulo recto, es decir, 90º.

ÁNGULOS SUPLEMENTARIOS
Son los ángulos que sumados valen dos ángulos rectos, es decir, 180º.

ÁNGULOS OPUESTOS POR EL VÉRTICE
Son dos ángulos tales que los lados de uno de ellos son las prolongaciones de los lados del otro.
"RECTAS PARALES Y UNA SECANTE"
Las paralelas son dos rectas que no se cruzan en ningún punto del plano. Si por el contrario, tenemos dos rectas que se cortan, estamos hablando de rectas secantes.
Cuando las rectas se cortan, forman 4 regiones llamadas ángulos. Cada
ángulo está limitado por dos lados y un vértice. Si las rectas se cortan
formando cuatro ángulos iguales, se dice que son rectas
perpendiculares.
 "ÁNGULOS DETERMINADOS POR RECTAS PARALELAS CORTADAS POR UNA SECANTE"
"ÁNGULOS DETERMINADOS POR RECTAS PARALELAS CORTADAS POR UNA SECANTE"
Las recta r corta a las rectas paralelas m y n:
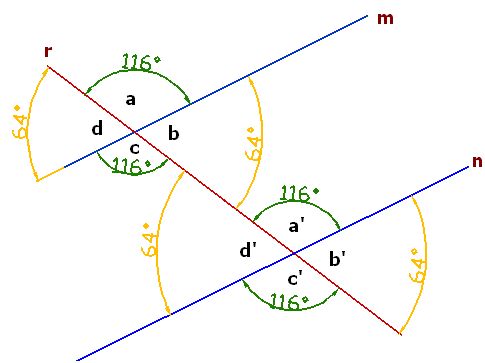
Los nombres de los ángulos según el lugar que ocupan reciben los nombres:
Interiores o internos:
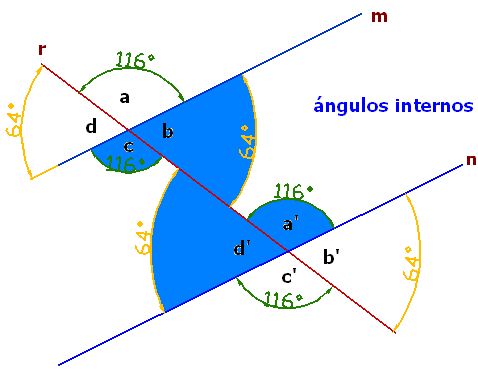
En azul, son los que se encuentran entre las rectas paralelas.
Ángulos exteriores o externos:

Los ángulos exteriores o externos en color violeta, son los que hallan en la zona exterior de las paralelas.
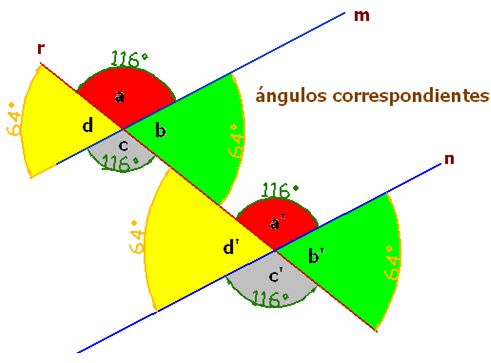
Ángulos correspondientes:
Son los que se encuentran en el mismo lado de la secante, un ángulo en la parte interior y otro en el exterior de las paralelas.
Son los que se encuentran en el mismo lado de la secante, un ángulo en la parte interior y otro en el exterior de las paralelas.
Los ángulos del mismo color son correspondientes:
El ángulo a se corresponde con el ángulo a’
El ángulo b se corresponde con el ángulo b’
El ángulo c se corresponde con el ángulo c’
El ángulo d se corresponde con el ángulo d’
El ángulo a se corresponde con el ángulo a’
El ángulo b se corresponde con el ángulo b’
El ángulo c se corresponde con el ángulo c’
El ángulo d se corresponde con el ángulo d’
Teniendo en cuenta lo dicho hasta aquí y fijándonos en la figura podemos afirmar que los ángulos correspondientes son iguales entre sí.
Ángulos alternos internos
Son los que se encuentran a distinto lado de la secante y en la zona interior de las rectas paralelas:
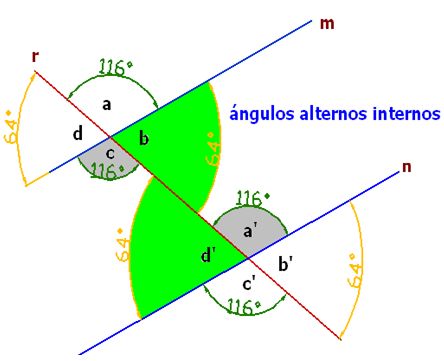
Los ángulos internos son d’, c, b y a’. Si los tomamos alternadamente, tendríamos, por un lado, los ángulos d’ y b, y por otro, c y a’ y comprobarás que los alternos internos son iguales entre sí.
Ángulos alternos externos:
Son los que se encuentran a distinto lado de la secante y en la zona externa de las rectas paralelas:
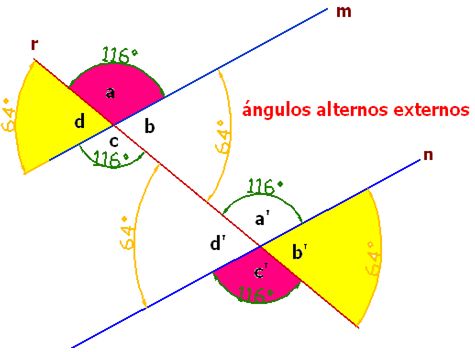
Los ángulos externos son: a, b’, c’ y d que tomándolos alternadamente tendremos, por un lado los ángulos a y c’, y por otro, los ángulos b’ y d. Comprobarás que los ángulos alternos externos son iguales entre sí.
"ÁNGULOS INTERIORES Y EXTERIORES"
En un triángulo existen dos tipos de ángulos:

Los ángulos interiores lo forman dos lados.
Los ángulos exteriores lo forman un lado y su prolongación.
Propiedades de los ángulos de triángulo
1. La suma de los ángulos interiores de un triángulo es igual a 180°.
A + B + C = 180º
2. El valor de un ángulo exterior de un triángulo es igual a la suma de los dos interiores no adyacentes.
α = B + C
3. Un ángulo interior y exterior de un triángulo son suplementarios, es decir, suman 180º.
α = 180º - A
"CONGRUENCIA DE TRIÁNGULOS"
Los criterios de congruencia de triángulos nos dicen que no es necesario verificar la congruencia de los 6 pares de elementos ( 3 pares de lados y 3 pares de ángulos), bajo ciertas condiciones, podemos verificar la congruencia de tres pares de elementos.Primer criterio de congruencia: LLL
Dos triángulos son congruentes si sus tres lados son respectivamente iguales.
a ≡ a’
b ≡ b’
c ≡ c’
→ triáng ABC ≡ triáng A’B'C’

Segundo criterio de congruencia: LAL
Dos triángulos son congruentes si son respectivamente iguales dos de sus lados y el ángulo comprendido entre ellos.
b ≡ b’
c ≡ c’
α ≡ α’
→ triáng ABC ≡ triáng A’B'C’

Tercer criterio de congruencia: ALA
Dos triángulos son congruentes si tienen un lado congruente y los ángulos con vértice en los extremos de dicho lado también congruentes. A estos ángulos se los llama adyacentes al lado.
b ≡ b’
α ≡ α’
β ≡ β’
→ triáng ABC ≡ triáng A’B'C’

Cuarto criterio de congruencia: LLA
Dos triángulos son congruentes si tienen dos lados respectivamente congruentes y los ángulos opuestos al mayor de los lados también son congruentes.
a ≡ a’
b ≡ b’
β ≡ β’
→ triáng ABC ≡ triáng A’B'C’

"SEMEJANZA DE TRIÁNGULOS"
Dos triángulos son semejantes si tienen sus ángulos respectivamente congruentes y si sus lados homólogos son proporcionales. (Lados homólogos son los opuestos a ángulos iguales) Es decir:



El
teorema de semejanza de triángulos dice en pocas palabras que son
triángulos semejantes aquellos que tienen la misma "forma", sólo son
diferentes en tamaño: un triángulo es más grande que el otro. El
enunciado textual de este teorema dice lo siguiente:
"Dos triángulos son semejantes si todos sus lados son respectivamente
proporcionales; o bien, son semejantes si tienen todos sus ángulos
respectivamente iguales"
"TEOREMA DE TALES"
"Si dos rectas cualesquieras se cortan por varias rectas paralelas, los
segmentos determinados en una de las rectas son proporcionales a los
segmentos correspondientes en la otra."

